Details
-
Type:
Bug
-
Status: Resolved (View Workflow)
-
Priority:
Major
-
Resolution: Fixed
-
Component/s: analysis-collector-plugin, dashboard-view-plugin
-
Labels:None
-
Similar Issues:
Description
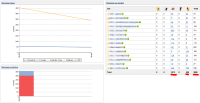
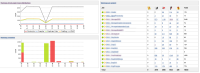
The trend "Warnings trend graph (type distribution)" in a Dashboard view displays average count instead of sum.
Example:
I have 2 Jobs, one has 50 findbugs warnings, the other 200.
If I put both of them in a dashboard view with a Portlet "Warnings trend graph (type distribution)" the count displayed is 125 instead of 250.
I don't know if this is a bug or a rfe...
But it would be useful to display the sum instead of average in trends
NB:
In the "Warnings per project" portlet the total is 250.
This problem may exists for the other warnings kind (compiler: yes, pmd: ?, etc...)
Attachments
Activity
I also prefer the first approach to compute the value for a job with several builds a day (this is already implemented
. However, I'm not sure if it makes much sense to count jobs on days without a valid build (e.g., no checkin on that day) as zero warnings, I think reusing the value from a previous build/day (with a valid result) makes more sense. Otherwise the number of warnings decreases by a large amount even thought nothing has changed in the source code. What do you think?
Yes you are right.
That seems more logic !
ebann
added a comment - Yes you are right.
That seems more logic ! If you are interested in testing the pre-release build, it is available at: http://faktorzehn.org:8081/job/Hudson%20Plug-ins%20(Compile)/75/
You need to install the analysis-core and the individual checker plug-ins.
Well, I think there is (at least) two solutions which both are interesting.
---- SOLUTION ONE -----
Average per day:
This solution shows the average warnings per day.
Which means that it may differ from the warnings value for a given time.
Day 0 = average(sum(JobA.day0.builds)) + average(sum(JobB.day0.builds)) + ...
Day 1 = average(sum(JobA.day1.builds)) + ...
As the X axis is a /day axis.
And failed/canceled jobs should be excluded (I don't want to see my code quality to be good when there are more fails than sucess)
For example:
Day 0:
+ JobA
-> build 1 = 500 warnings
-> build 2 = 1000 warnings
+ JobB
-> build 1 = 500 warnings
-> build 2 = FAILURE
Day 1:
+ JobA
-> build 1 = 1000 warnings
-> build 2 = 1000 warnings
+ JobB
-> NO BUILD or FAILURE
Day 2:
+ JobA
-> build 1 = 1000 warnings
-> build 1 = 5000 warnings
-> build 2 = 0 warnings
+ JobB
-> build 1 = 500 warnings
-> build 1 = 5000 warnings
-> build 2 = 0 warnings
Would give:
Day 0 = (500+1000)/2 + 500/1 = 1250 warnings. (REAL (at the end of the day) = 1500)
Day 1 = (1000+1000)/2 + 0 = 1000 warnings. (REAL (at the end of the day) = 1000)
Day 2 = (1000+5000+0)/2 + (500 5000 0)/2 = 5750 warnings. (REAL (at the end of the day) = 0)
---- SOLUTION TWO -----
Instant value:
This solution shows the last value of the day.
Which means that it should be equals to the warnings value at a given time.
Day 0 = last(JobA.day0.builds) + last(JobB.day0.builds) + ...
Day 1 = last(JobA.day1.builds) + ...
And failed/canceled jobs should be excluded (I don't want to see my code quality to be good when there are more fails than sucess)
For example:
Day 0:
+ JobA
-> build 1 = 500 warnings
-> build 2 = 1000 warnings
+ JobB
-> build 1 = 500 warnings
-> build 2 = FAILURE
Day 1:
+ JobA
-> build 1 = 1000 warnings
-> build 2 = 1000 warnings
+ JobB
-> NO BUILD or FAILURE
Day 2:
+ JobA
-> build 1 = 1000 warnings
-> build 2 = 0 warnings
+ JobB
-> build 1 = 500 warnings
-> build 2 = 0 warnings
Would give:
Day 0 = last(500,1000) + last(500) = 1500 warnings. (REAL (at the end of the day) = 1500)
Day 1 = last(1000,1000) + last(0) = 1000 warnings. (REAL (at the end of the day) = 1000)
Day 2 = last(1000,5000,0) + last(500,5000,0) = 0 warnings. (REAL (at the end of the day) = 0)
Well, this is a bit more "complex" that what i guessed first
Maybe there could be the 2 solutions as different graph. (DAY_AVERAGE, DAY_INSTANT)
If not, I would prefer the first one which seems shows more about what happened each day...
But that's my opinion...